Topic 1 - Vectors

Scalar and Vector quantities

There are many quantities you have heard about that can be fully described by some number and appropriate unit of measurement, such as mass (e.g. \(10\text{ g}\)), distance between two points (e.g. \(0.5\text{ m}\)) and time take for a kettle to boil (e.g. \(120\text{ s}\) or \(2\text{ mins}\)). We call these types of quantities scalars and the size of the scalar is the magnitude. However there are other quantities that are not completely characterised by a single number with units.

Consider the example where I told you that a person started half way between the entrance to the Hicks building and John’s Van[1], and that the person walked 4 meters. You do not have enough information to find their final position, and whether they walked towards getting a tasty treat or in some other direction. It is this word direction that is needed to provide the complete characterisation of displacement: the length, direction and units of the distance travelled allows you to know where the person is. We call this type of quantity a vector.

Note

A vector is defined to be any quantity which is completely specified by a scalar magnitude and a direction.

Notation convention

Note

Strictly speaking the displacement or magnitude of \(\overrightarrow{OA}\) is \(\left|OA\right|\) where the \(| |\) represents the modulus of a quantity.

There are a number of different ways in which a vector quantity can written. One common method is known as the over-arrow style, for reasons that will become clear very quickly. If we have a particle that is starting at some point \(O\) and moves to some final position \(A\) then the displacement of the particle is denoted by \(OA\). Given that a vector also has some direction to it we can represent this by introducing an arrow such that the vector describing the displacement from point \(O\) to point \(A\) is \(\overrightarrow{OA}\).

Two other complementary notation styles exist where the vector is described by a single letter or variable rather than the start and end points, and present this letter either in bold or with a line underneath. So if our single letter choice to represent the vector between points \(O\) and \(A\) was \(a\) then we would write

\[\overrightarrow{OA} = \mathbf{a} = \underline{a}\]

I have described these two styles as complementary as they depend on the tool you are using to write them. In creating these digital typed notes I can easily turn an letter into bold font but this is harder to do with handwritten letters, and so when writing vectors by hand the underline style is more common.

The magnitude of a vector using this single letter notation is usually represented by the same letter but in italics rather than bold, meaning

\[|\overrightarrow{OA}| = \left|\mathbf{a}\right| = a\]

Finally, for the most part the choice of vector notation is a matter of personal preference but you’ll find that as you progress in your studies the bold type notation is probably the most likely to be used. As you’ve gathered from the above it’s the one that I tend to use and so will be the preferred choice going forward but I may swap between conventions as deemed appropriate.

Worked Example 1

Question

A student starts at the point \(O\) and walks \(4.0\text{ km}\) east to the point \(A\) and the \(3.0\text{ km}\) north to the point \(B\).

Find their final displacement from point \(O\).

Hint

1. It helps to draw this out (it does not have to be to scale).

2. Pay attention to the type of triangle that this forms.

Solution

By drawing this out the two stages of the journey form two sides of a right angle triangle, with the hypoteneuse being the displacement we are interested in.

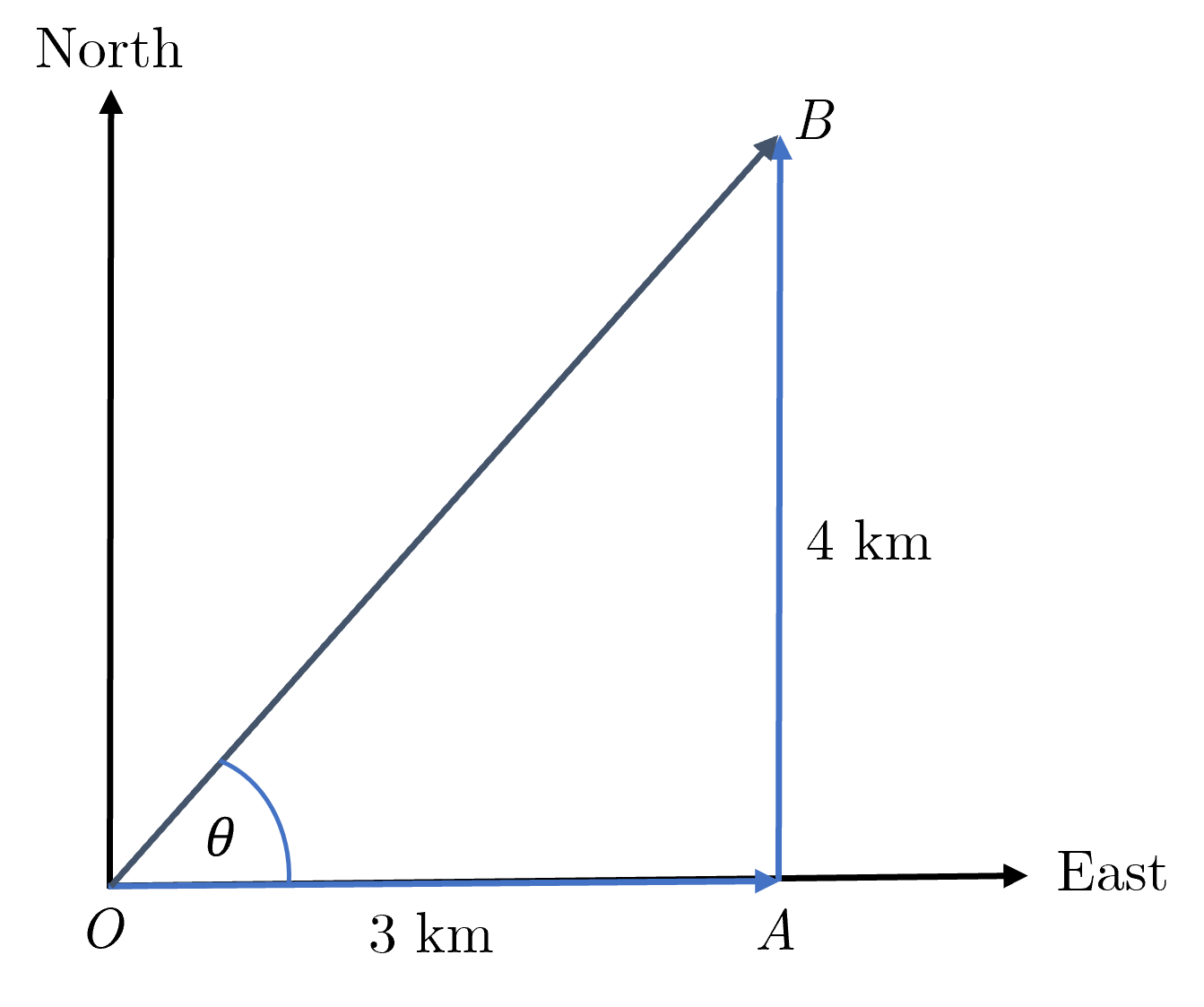
Using Pythagoras’ Theorem:

\[\begin{align*} OB^2 &= OA^2 + AB^2\\ &= 4.0^2 + 3.0^2\\ &= 16.0 + 9.0 = 25.0\\ \therefore |OB| = 5.0 \end{align*}\]

This \(|OB|\) is the distance the person has travelled, and to find the displacement we also need the direction which can be determined using trigonometry, and is defined as \(\theta\) in the diagram. As all sides are known we can use any of the identities but I will choose the two values given in the question and the tangent relationship:

\[\begin{align*} \tan\theta &= \frac{\text{opposite}}{\text{adjacent}}\\ &= \frac{3.0}{4.0}\\ \therefore \theta &= \tan^{-1}\left(\frac{3.0}{4.0}\right) \approx 36.9^\circ \end{align*}\]

Properties of vectors

Equal vectors

Two vectors are equal if an only if they have both the same magnitude and the same direction. In the diagram to the right two vectors are shown as the arrows correcting start and end points, and we can see that \(\mathbf{x} = \mathbf{y}\), or in the arrow notation \(\overrightarrow{AB}=\overrightarrow{PQ}\).

It’s important to note that the two vectors \(\mathbf{x}\) and \(\mathbf{y}\) are equal even though they have different start and end points. What is the same is the distance between the two start and ends, and the direction from start to end, but two vectors do not have to share a start and end point to be equal.

Similar vectors

A vector can be equal and opposite to another if the size of the vector was the same but it is pointing in the opposite direction. In the case of the diagram above the second vector could instead start at point \(Q\) and end at point \(P\). In this case we would state that \(\mathbf{y}=-\mathbf{x}\). If you are using the arrow notation style the order of letters is crucial: \(\overrightarrow{PQ}\) is not the same as \(\overrightarrow{QP}\), and in fact \(\overrightarrow{PQ} = -\overrightarrow{QP}\).

We can also have vectors that point in the same direction (i.e. they are parallel) but have different magnitudes as shown below.

From this we can state that:

\[\begin{align*} \overrightarrow{PQ} &= k\overrightarrow{LM} \end{align*}\]

where \(k\) is a scalar that represents the scaling factor between the two vectors which can be written as

\[\begin{align*} k &= \frac{|\overrightarrow{PQ}|}{|\overrightarrow{LM}} \end{align*}\]

Worked Example 2

Question

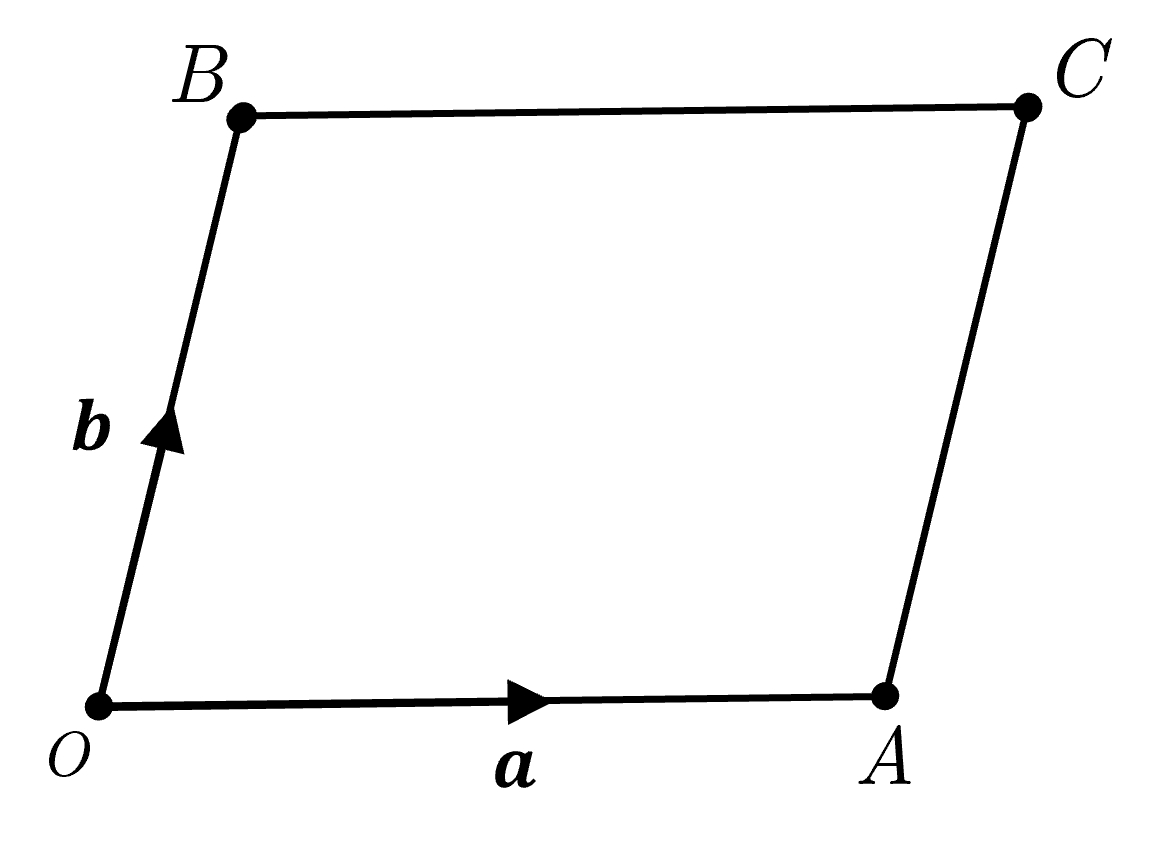
The diagram shows a parallelogram \(OABC\), with \(\overrightarrow{OA}=\mathbf{a}\) and \(\overrightarrow{OB}=\mathbf{b}\). The point \(D\) is the mid-point of \(AC\). Express the following vectors in terms of \(\mathbf{a}\) and \(\mathbf{b}\).

1. \(\overrightarrow{BC}\)

2. \(\overrightarrow{AC}\)

3. \(\overrightarrow{CA}\)

4. \(\overrightarrow{OC}\)

5. \(\overrightarrow{AB}\)

6. \(\overrightarrow{OD}\)

Hint

1. Remember that a vector pointing in the opposite direction of a similar one has a minus sign in front, i.e. \(\overrightarrow{XY}=-\overrightarrow{YX}\).

2. Use the scaling factor \(k\) to ‘travel’ some contraction (\(k<1\)) or stretch (\(k>1\)) of a vector.

Solution

1. \(\overrightarrow{BC}\) is in the same direction as \(\overrightarrow{OA}\) and of the same length because \(OABC\) is a parallelogram. Therefore \(\overrightarrow{BC}=\overrightarrow{OA}=\mathbf{a}\).

2. Similarly, \(\overrightarrow{AC}\) is in the same direction and of the same size as \(\overrightarrow{OB}\) and so \(\overrightarrow{AC}=\overrightarrow{OB}=\mathbf{b}\).

3. The vector \(\overrightarrow{CA}\) is the same length as \(\overrightarrow{AC}\) but in the opposite direction, and therefore \(\overrightarrow{CA} = -\overrightarrow{AC}=-\mathbf{b}\).

4. To find \(\overrightarrow{OC}\) consider the triangle \(OAC\).

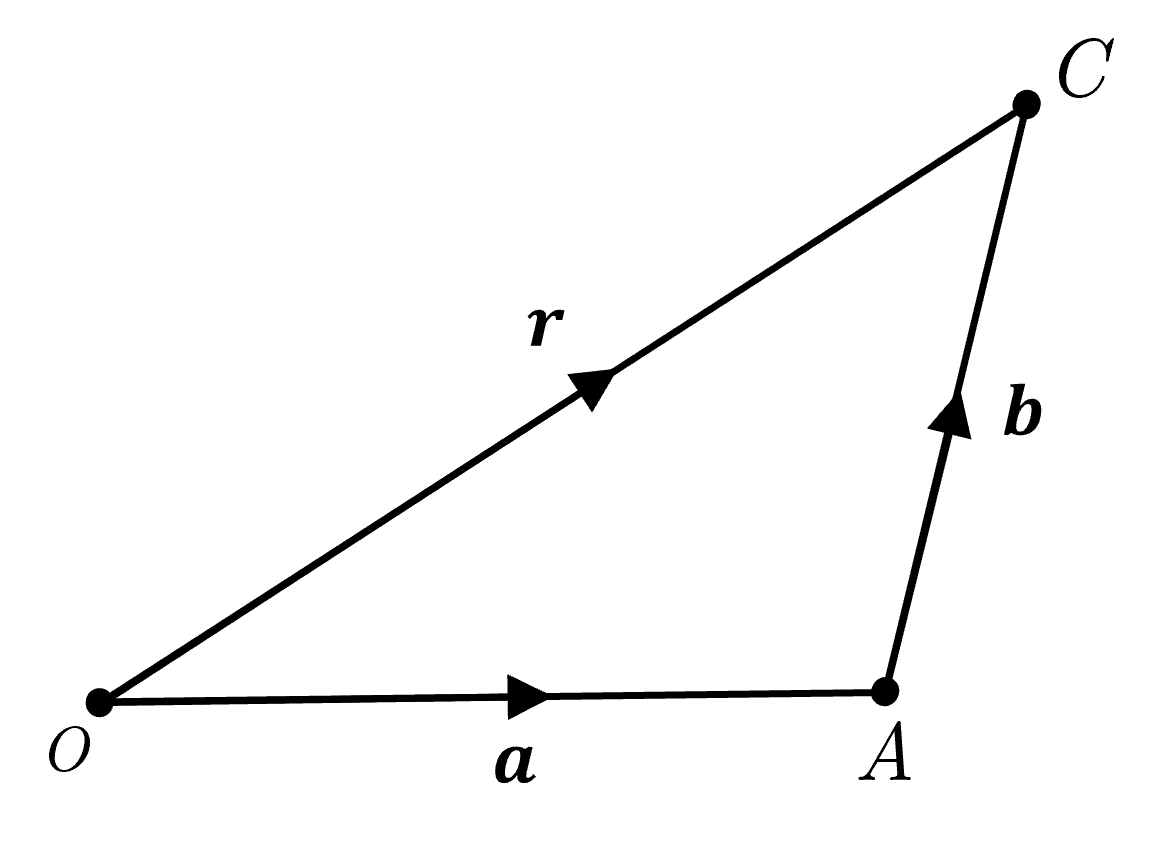
By the triangle law:

\[\begin{align*} \overrightarrow{OC} &= \overrightarrow{OA} + \overrightarrow{AC}\\ &= \overrightarrow{OA} + \overrightarrow{OB}\\ &= \mathbf{a} + \mathbf{b} \end{align*}\]

5. To find \(\overrightarrow{AB}\) consider the triangle \(OAB\).

By the triangle laaw:

\[\begin{align*} \overrightarrow{AB} &= \overrightarrow{AO} + \overrightarrow{OB}\\ &= -\overrightarrow{OA} + \overrightarrow{OB}\\ &= -\mathbf{a} + \mathbf{b} = \mathbf{b} - \mathbf{a} \end{align*}\]

6. To find \(\overrightarrow{OD}\) consider the triangle \(OAD\).

We must first find \(\overrightarrow{AD}\). \(\overrightarrow{AD}\) is parallel to \(\overrightarrow{AC}\) (shown in grey) and half its length as \(D\) is the midpoint of \(\overrightarrow{AC}\), so

\[\begin{align*} \overrightarrow{AD} &= \frac{1}{2}\mathbf{b} \end{align*}\]

By the triangle law:

\[\begin{align*} \overrightarrow{OD} &= \overrightarrow{OA}+\overrightarrow{AD}\\ &= \mathbf{a} + \frac{1}{2}\mathbf{b} \end{align*}\]

Addition (and subtraction) of vectors

Suppose that runner 1 goes from a point \(O\) to \(A\) and then from point \(A\) to point \(B\), and runner 2 goes directly from point \(O\) to point \(B\). As the result of these two different journeys is the same (they start and end at the same point) we can write

\[\begin{align*} \text{Runner 1} &= \text{Runner 2}\\ \overrightarrow{OA}+\overrightarrow{AB} &= \overrightarrow{OB}\\ \text{or }\qquad \mathbf{x} + \mathbf{y} &= \mathbf{r} \end{align*}\]

The displacement \(\mathbf{r}=\overrightarrow{OB}\) is the sum or resultant of the displacements \(\mathbf{x}=\overrightarrow{OA}\) and \(\mathbf{y}=\overrightarrow{AB}\). This is sometimes known as the triangle law of addition, but it also holds true for a single vector being the resultant of the sum of any number of other vectors.

Cartesian unit vectors and components

A unit vector is a vector with magntitude of 1 unit. They are particularly useful in allowing us to specify the direction of some property (force, velocity, etc) without changing the magnitude of the property itself: multiplying a value by a unit vector does not change the magnitude but provides additional information about the direction via the direction of the unit vector. There are a number of unit vector sets that are particularly helpful in physics. The one we will use in this course is known as the Cartesian set as the unit vectors lie along the positive cartesian axes, more commonly known as the \(x\) and \(y\) axes in two dimensions with the \(z\) axis taking us into three dimensions.

Any vector can be written as the product of the magnitude of the vector times the unit vector pointing in the same direction as the original vector. So for the general vector \(\mathbf{a}\):

\[\begin{align*} \mathbf{a} &= |\mathbf{a}|\,\hat{\mathbf{a}} \end{align*}\]

Notation

Unit vectors are commonly represented by use of the ^ or “hat” symbol. For example the unit vector of some vector \(\mathbf{a}\) is written as \(\hat{\mathbf{a}}\).

\(\hat{\mathbf{i}},\hat{\mathbf{j}}\) notation.

Note

The unit vector in the \(z\) direction is \(\hat{\mathbf{k}}\).

The unit vectors along the \(x\) and \(y\) cartersian axes are usually denoted by \(\hat{\mathbf{i}}\) and \(\hat{\mathbf{j}}\) respectively. So the vector \((3\hat{\mathbf{i}}+4\hat{\mathbf{j}})\) corresponds to a displacement of 3 units in the \(x\) direction (i.e. in the direction of the unit vector \(\hat{\mathbf{i}}\)) and 4 units in the \(y\) direction (i.e. in the direction of the unit vector \(\hat{\mathbf{j}}\)).

The use of unit vectors along the cartesian axes is very useful as we can describe any single vector in terms of independent \(x\) and \(y\) components. This in turn means we can add vectors together using this notation by adding the relevant components separately. If we want to add vectors together we add the terms involving \(\hat{\mathbf{i}}\) and those involve \(\hat{\mathbf{j}}\) separately. Expressing this mathematically for two general vectors \(\mathbf{a}=a_1\hat{\mathbf{i}}+a_2\hat{\mathbf{j}}\) and \(\mathbf{b}=b_1\hat{\mathbf{i}} + b_2\hat{\mathbf{j}}\) (where \(a_1,a_2,b_1,b_2\) are arbitrary constants) their sum would be

\[\begin{align*} \mathbf{a} + \mathbf{b} &= (a_1\hat{\mathbf{i}} + a_2\hat{\mathbf{j}}) + ((b_1\hat{\mathbf{i}} + b_2\hat{\mathbf{j}})\\ &= (a_1\hat{\mathbf{i}} + b_1\hat{\mathbf{i}}) + (a_2\hat{\mathbf{j}} + b_2\hat{\mathbf{j}})\\ &= (a_1 + b_1)\hat{\mathbf{i}} + (a_2 + b_2)\hat{\mathbf{j}} \end{align*}\]

Worked Example 3

Question

Given \(\mathbf{a}=(2\hat{\mathbf{i}} + 3\hat{\mathbf{j}})\) and \(\mathbf{b} = (4\hat{\mathbf{i}} - 2\hat{\mathbf{j}})\), find \(\mathbf{a} + \mathbf{b}\) in terms of \(\hat{\mathbf{i}}\) and \(\hat{\mathbf{j}}\). Show that this result is true by plotting \(\mathbf{a}\), \(\mathbf{b}\) and \(\mathbf{a+b}\) on a graph.

Hint

When adding two vectors together you should add only the relevant components together. In this case treat \(\hat{\mathbf{i}}\) and \(\hat{\mathbf{j}}\) components separately.

Solution

Given \(\mathbf{a}=(2\hat{\mathbf{i}} + 3\hat{\mathbf{j}})\) and \(\mathbf{b} = (4\hat{\mathbf{i}} - 2\hat{\mathbf{j}})\) then

\[\begin{align*} \mathbf{a} + \mathbf{b} &= (2\hat{\mathbf{i}} + 3\hat{\mathbf{j}}) + (4\hat{\mathbf{i}} - 2\hat{\mathbf{j}})\\ &= (2{\mathbf{i}} + 4{\mathbf{i}}) + (3{\mathbf{j}} - 2{\mathbf{j}})\\ &= 6{\mathbf{i}} + {\mathbf{j}} \end{align*}\]

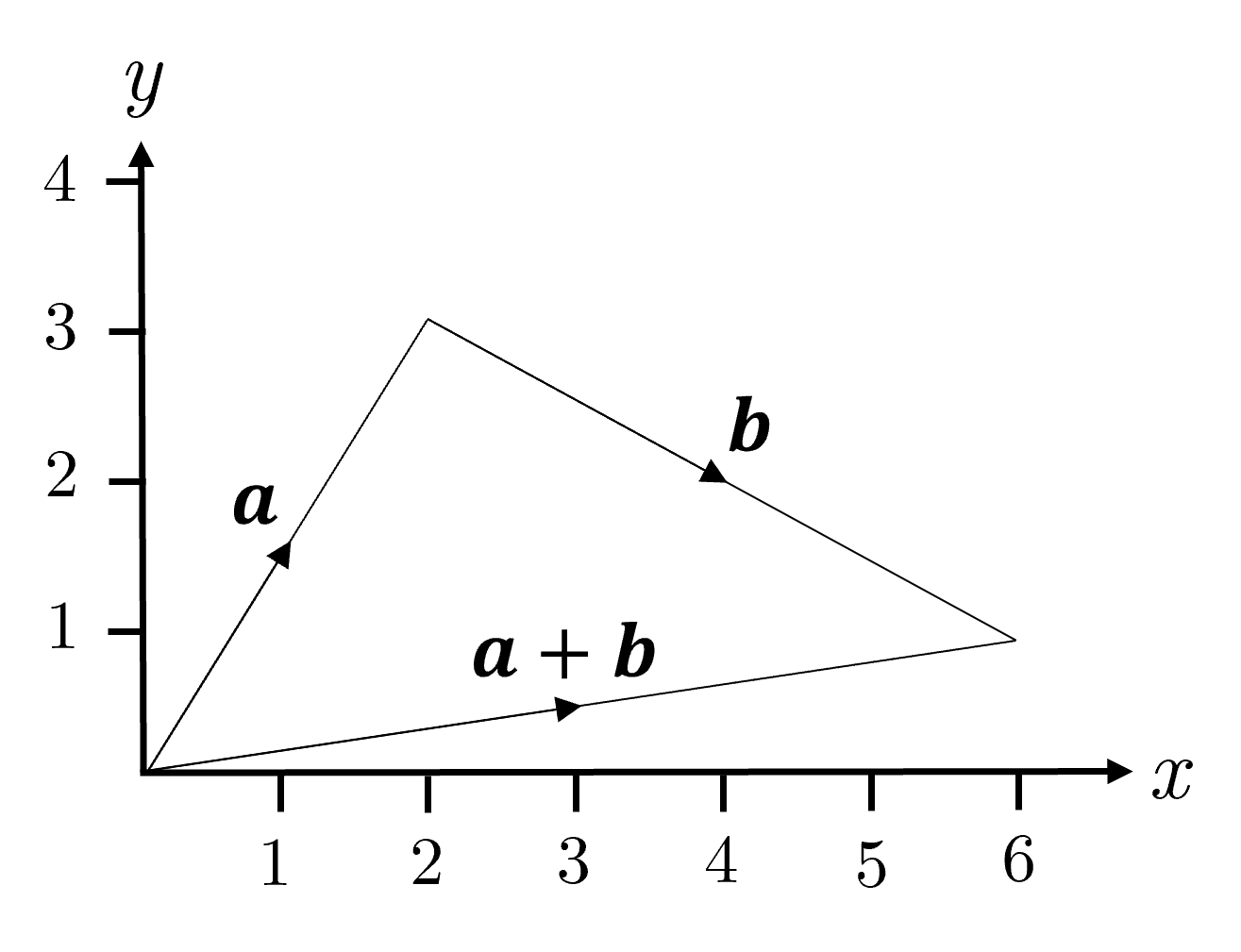
Subtraction of vectors with the \(\hat{\mathbf{i}},\hat{\mathbf{j}}\) notation works in a similar way, by subtracting the \(\hat{\mathbf{i}}\) and \(\hat{\mathbf{j}}\) components separately. For two general vectors \(\mathbf{a}=a_1\hat{\mathbf{i}}+a_2\hat{\mathbf{j}}\) and \(\mathbf{b}=b_1\hat{\mathbf{i}} + b_2\hat{\mathbf{j}}\) (where \(a_1,a_2,b_1,b_2\) are arbitrary constants) their difference would be

\[\begin{align*} \mathbf{a} - \mathbf{b} &= (a_1\hat{\mathbf{i}} + a_2\hat{\mathbf{j}}) - ((b_1\hat{\mathbf{i}} + b_2\hat{\mathbf{j}})\\ &= (a_1\hat{\mathbf{i}} - b_1\hat{\mathbf{i}}) + (a_2\hat{\mathbf{j}} - b_2\hat{\mathbf{j}})\\ &= (a_1 - b_1)\hat{\mathbf{i}} + (a_2 - b_2)\hat{\mathbf{j}} \end{align*}\]

Magnitude of a vector in \(\hat{\mathbf{i}},\hat{\mathbf{j}}\) notation.

When a vector \(\mathbf{R}\) is given in terms of the unit vectors \(\hat{\mathbf{i}}\) and \(\hat{\mathbf{j}}\) you can find its magnitude by using Pythagoras’ Theorem because \(\hat{\mathbf{i}}\) and \(\hat{\mathbf{j}}\) are perpendicular so their components form two sides of a right angle triangle.

If \(\mathbf{R} = x\hat{\mathbf{i}} +y\hat{\mathbf{j}}\) then

\[\begin{align*} |\mathbf{R}|^2 &= |\mathbf{x}|^2 + |\mathbf{y}|^2\\ \therefore R^2 &= \sqrt{x^2 + y^2} \end{align*}\]

Worked Example 4

Question

Find the unit vector in the direction of the vector \(\mathbf{a} = 2\hat{\mathbf{i}} + 3\hat{\mathbf{j}}\).

Hint

Recall that any vector is the product of the magnitude of the vector and the unit vector pointing in the same direction.

Solution

The magnitude of \(\mathbf{a}\) is

\[\begin{align*} |\mathbf{a}| &= \sqrt{2^2 + 3^2}\\ &= \sqrt{13} \end{align*}\]

So the unit vector pointing in the same direction as \(\mathbf{a}\) is

\[\begin{align*} \frac{\mathbf{a}}{|\mathbf{a}|} &= \frac{1}{\sqrt{13}}(2\hat{\mathbf{i}} + 3\hat{\mathbf{j}})\\ &= \frac{2}{\sqrt{13}}\hat{\mathbf{i}} + \frac{3}{\sqrt{13}}\hat{\mathbf{j}} \end{align*}\]

Components of a vector

Note

In two dimensions this will be a pair of vectors, and in three dimensions we need three in the set.

We’ve already seen that we can combine two vectors into a single resultant vector, but it is useful to do the reverse where we express a single vector by an equivalent set of vectors. This is known as resolving a vector into component vectors, and our choice of components should be aligned with some sort of defined coordinate axis. For most of the systems we will see in this course the most appropriate coordinate system will be the cartesian one meaning we resolve our vector into \(\hat{\mathbf{i}}\) and \(\hat{\mathbf{j}}\) components.

Look at the situation shown in Fig. 1.

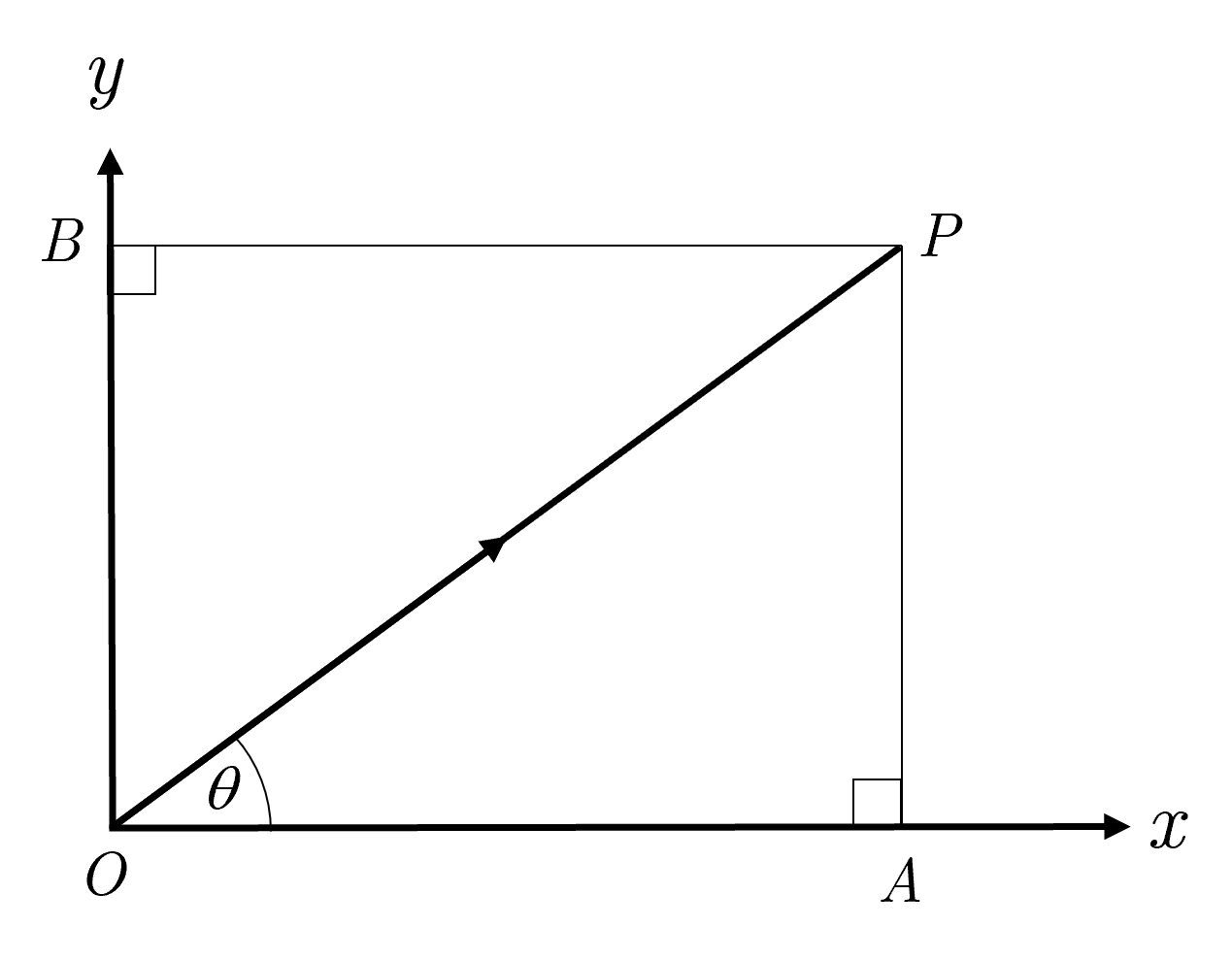
Fig. 1 Resolving one vector \((\overrightarrow{OP})\) into two component vectors \((\overrightarrow{OA},\overrightarrow{AP})\) aligned along the cartesian axes.

By the triangle rule of addition we can state that

\[\begin{align*} \overrightarrow{OP} &= \overrightarrow{OA} + \overrightarrow{AP}\\ &= \overrightarrow{OA} + \overrightarrow{OB} \end{align*}\]

By trigonometry:

\[\begin{align*} \frac{OA}{OP} &= \cos\theta \implies OA = OP\cos\theta\\ \frac{OB}{OP} &= \sin\theta \implies OB = OP\sin\theta \end{align*}\]

And so

\[\begin{align*} \overrightarrow{OA} &= OP\cos\theta\hat{\mathbf{i}}\\ \overrightarrow{OB} &= OP\sin\theta\hat{\mathbf{j}}\\ \therefore \overrightarrow{OP} &= (OP\cos\theta)\hat{\mathbf{i}} + (OP\sin\theta)\hat{\mathbf{j}} \end{align*}\]

\(OP\cos\theta\) and \(OP\sin\theta\) are called the cartesian components of \(\overrightarrow{OP}\).

Using vectors in mechanics

Position vectors

Imagine a particple \(P\) moving in a plane that has some fixed point \(O\) on it. The position of \(P\) with respect to this fixed point \(O\) is uniquely defined by the vector

\[\begin{align*} \overrightarrow{OP} &= \mathbf{r} \end{align*}\]

where \(\mathbf{r}\) is the position vector of \(P\) relative to \(O\). The choice of the letter \(O\) is intentional because we often (but not always) use the origin as the position reference point to which we define position vectors to.

The general form of the vector between the reference point with coordinates \((O_x,O_y)\) and the position point with coordinates \((P_x,P_y)\) is:

\[\begin{align*} \mathbf{r} &= (P_x-O_x)\hat{\mathbf{i}}+(P_y-O_y)\hat{\mathbf{j}} \end{align*}\]

Worked Example 5

Question

At a given time the cartesian coordinates of the position \(P\) of a particle are \((2,1)\). Find the position vectors of \(P\)

1. relative to the origin.

2. relative to the point \((1,2)\)

Hint

1. Start by drawing a set of cartesian axes, adding the three key points, and finally connecting the pairs of points with directional lines (i.e. lines with arrows).

Solution

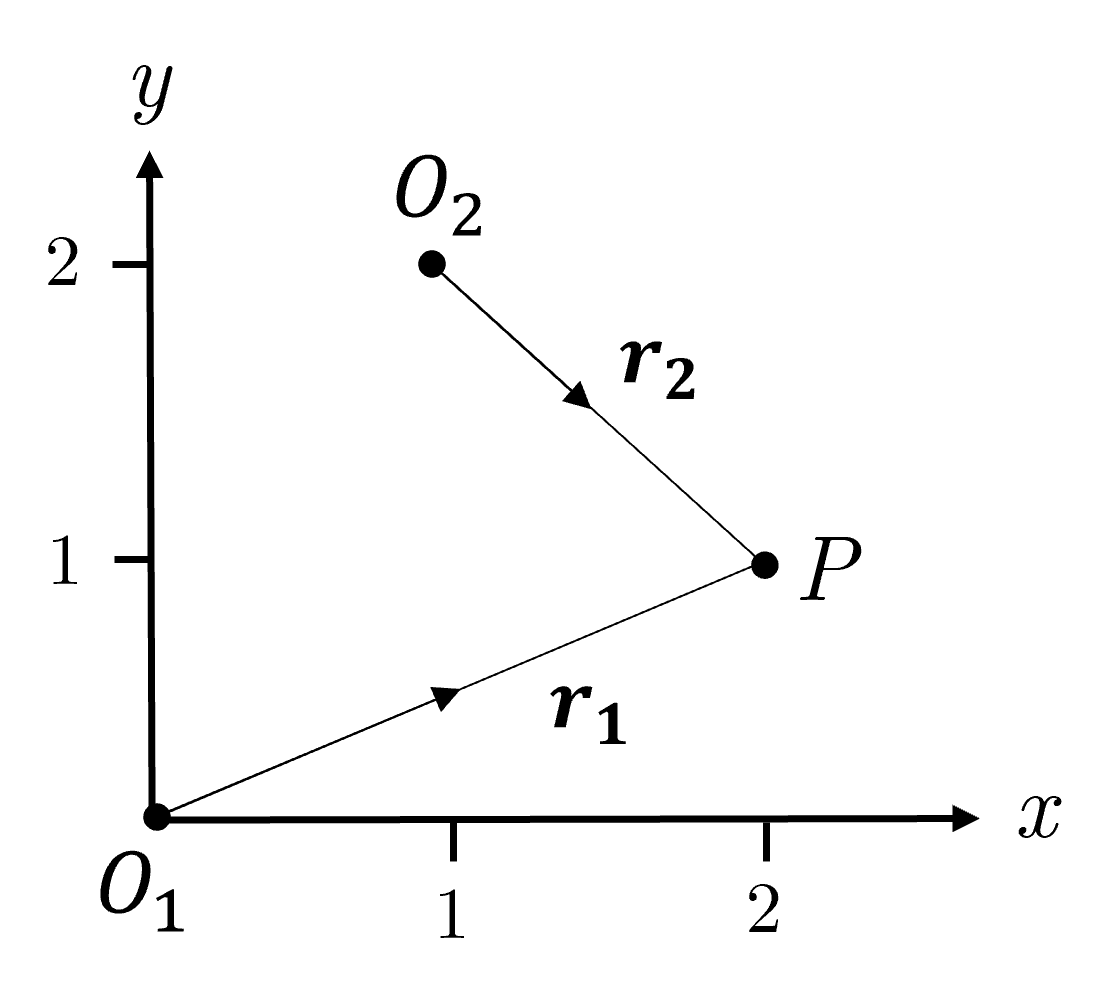
In the diagram point \(P\) is labelled at position \((2,1)\), and the two starting points \(O_1\) and \(O_2\) are at the origin and position \((1,2)\) respectively.

1. The position vector \(\mathbf{r}_1\) of point \(P\) with respect to the origin \(O_1\) is

\[\begin{align*} \textbf{r}_1 &= \overrightarrow{O_1P}\\ &= (2-0)\hat{\mathbf{i}} + (1-0)\hat{\mathrm{j}}\\ &= 2\hat{\mathbf{i}} + 1\hat{\mathrm{j}} \end{align*}\]

2. The position vector \(\mathbf{r}_2\) of point \(P\) with respect to the point \(O_2\) is

\[\begin{align*} \textbf{r}_2 &= \overrightarrow{O_2P}\\ &= (2-1)\hat{\mathbf{i}} + (1-2)\hat{\mathrm{j}}\\ &= 1\hat{\mathbf{i}} - 1\hat{\mathrm{j}} \end{align*}\]

Velocity and acceleration vectors

If a particle is moving with a speed of \(5\text{ m s}^{-1}\) then, provided the speed remains constant, it will travel \(5\text{ m}\) every second, no matter what type of path the particle is travelling on. However to get a complete picture of what is happening you need to know the direction in which the particle is moving: if you only know the speed then you do know that the particle mentioned above will be \(5\text{ m}\) away from the starting point after one second, but you don’t know exactly where it is without knowing the direction this \(5\text{ m}\) distance was in. If we know the speed and direction of a particle we know its velocity, typically denoted by \(\mathbf{v}\):

Note

When you cover calculus you’ll see the formal definition of \(\mathbf{v}=\frac{\mathrm{d}\mathbf{r}}{\mathrm{d}t}\).

Note

The velocity of a particle is a vector in the direction of motion (i.e. in the same direction as the displacement vector) whose magnitude is equal to the speed of the particle.

\[\begin{align*} \text{velocity} = \frac{\text{change in displacement}}{\text{time}} \end{align*}\]

Just as the velocity of a particle tells you how the position (vector) of a particle changes with time, the acceleration describes how the velocity changes with time. As velocity is a vector so is acceleration, and is defined as

Note

Another calculus definition: \(\mathbf{a}=\frac{\mathrm{d}\mathbf{v}}{\mathrm{d}t}=\frac{\mathrm{d}^2\mathbf{r}}{\mathrm{d}t^2}\).

Note

Acceleration is the rate of change of velocity.

\[\begin{align*} \text{acceleration} = \frac{\text{change in velocity}}{\text{time}} \end{align*}\]

Scalars and vectors in Newtonian mechanics - summary

Summary table

Quantity	Type	Description
Distance	Scalar	Length of the path between two points
Speed	Scalar	Rate of change of distance
Mass	Scalar	Amount of matter in an object
Time	Scalar	Duration of an event
Energy	Scalar	Capacity to do work
Temperature	Scalar	Measure of thermal energy
Work	Scalar	Energy transferred by force over distance
Power	Scalar	Rate at which work is done
Potential Energy	Scalar	Energy stored due to position
Kinetic Energy	Scalar	Energy of an object due to its m otion
Volume	Scalar	Space occupied by a substance
Pressure	Scalar	Force per unit area
———————-	———	—————————————————-
Displacement	Vector	Change in position
Velocity	Vector	Rate of change of displacement
Acceleration	Vector	Rate of change of velocity
Force	Vector	Interaction that causes a cha nge in motion
Momentum	Vector	Product of mass and velocity
Impulse	Vector	Change in momentum
Position	Vector	Location of an object in spa ce
Angular Velocity	Vector	Rate of rotation
Torque	Vector	Tendency of a force to r ota
Angular momentum	Vector	Product of rotational inertia and angular velocity

---

[1]

an important landmark